La hidrodinamica es la parte de la hidraulica que se encarga de estudiar el comportamiento de los liquidos en movimiento. para ello se considera entre otras cosas la velocidad, la presion, el flujo y el gasto de liquido.
En el estudio dela hidrodinamica, el teorema de Bernoulli, que trata de la ley de la conservacion de la energia es de primordial importancia, pues señala que la suma de las energias cinética, potencial, y de presion de un liquido en movimiento en un punto determinado es igual a la de otro punto cualquiera.
La mecánica de fluidos investiga las propiedades de un fluido ideal sin friccion y tambien estudia las caracteristicas de un fluido viscoso en el cual se presenta friccion.
Un fluido es omprensible cuando su densidad varia de acuerdo con la presion que recibe; tal es el caso del aire y ortos gases estudiados por la aerodinamica.
La hidrodinámica estudia la dinámica de fluidos incompresibles. Por extensión, dinámica de fluidos.
Etimológicamente, la hidrodinámica es la dinámica del agua, puesto que el prefijo griego "hidro-" significa "agua". Aun así, también incluye el estudio de la dinámica de otros fluidos. Para ello se consideran entre otras cosas la velocidad, presión, flujo y gasto del fluido. Para el estudio de la hidrodinámica normalmente se consideran tres aproximaciones importantes:
- Que el fluido es un líquido incompresible, es decir, que su densidad no varía con el cambio de presión, a diferencia de lo que ocurre con los gases.
- Se considera despreciable la pérdida de energía por la viscosidad, ya que se supone que un líquido es óptimo para fluir y esta pérdida es mucho menor comparándola con la inercia de su movimiento.
- Se supone que el flujo de los líquidos es en régimen estable o estacionario, es decir, que la velocidad del líquido en un punto es independiente del tiempo.
La hidrodinámica tiene numerosas aplicaciones industriales, como diseño de canales, construcción de puertos y presas, fabricación de barcos, turbinas, etc.
El gasto o caudal es una de las magnitudes principales en el estudio de la hidrodinámica. Se define como el volumen de líquido ΔV que fluye por unidad de tiempo Δt. Sus unidades en el Sistema Internacional son los m3/s y su expresión matemática:
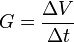
Esta fórmula nos permite saber la cantidad de líquido que pasa por un conducto en cierto intervalo de tiempo o determinar el tiempo que tardará en pasar cierta cantidad de líquido.
El principio de Bernoulli es una consecuencia de la conservación de la energía en los líquidos en movimiento. Establece que en un líquido incompresible y no viscoso, la suma de la presión hidrostática, la energía cinética por unidad de volumen y la energía potencial gravitatoria por unidad de volumen, es constante a lo largo de todo el circuito. Es decir, que dicha magnitud toma el mismo valor en cualquier par de puntos del circuito. Su expresión matemática es:
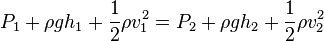
donde P es la presión hidrostática, ρ la densidad, g la aceleración de la gravedad, h la altura del punto y v la velocidad del fluido en ese punto. Los subíndices 1 y 2 se refieren a los dos puntos del circuito.
La otra ecuación que cumplen los fluidos no compresibles es la ecuación de continuidad, que establece que el caudal es constante a lo largo de toda el circuito hidráulico:
G = A1v1 = A2v2
donde A es el área de la sección del conducto por donde circula el fluido y v su velocidad media.
En el caso de fluidos compresibles, donde la ecuación de Bernouilli no es válida, es necesario utilizar la formulación más completa de Navier y Stokes. Estas ecuaciones son la expresión matemática de la conservación de masa y de cantidad de movimiento. Para fluidos compresibles pero no viscosos, también llamados fluidos coloidales, se reducen a las ecuaciones de Euler.
Daniel Bernoulli fue un matemático que realizó estudios de dinámica.
La hidrodinámica o fluidos en movimientos presenta varias características que pueden ser descritas por ecuaciones matemáticas muy sencillas.
Ley de Torricelli: si en un recipiente que no está tapado se encuentra un fluido y se le abre al recipiente un orificio la velocidad con que caerá ese fluido será:

La otra ecuación matemática que describe a los fluidos en movimiento es el número de Reynolds:
N = dVD / n
donde d es la densidad v la velocidad D es el diámetro del cilindro y n es la viscosidad dinámica.
Gasto_________________________________________________
El gasto es el volumen de un líquido que atraviesa una sección de un conductor en un segundo. Al gasto, también se le denomina flujo y su símbolo es: Q =Av donde A= área del conductor y v = velocidad con que fluye. También al gasto se le denomina en algunas ocasiones rapidez o velocidad de flujo.
Ejemplo:
Una llave tiene una sección de 4cm2 y proporciona un volumen de 30L en un minuto. Calcular a que equivale el gasto y la velocidad del líquido.
Q = v/t = 30000 cm3/60 seg = 500 cm3/seg
V = Q/A = 500 cm3/seg/4cm2 = 125 cm/seg
Flujo__________________________________________________
El flujo se define como la cantidad de masa del líquido que fluye a través de una tubería en un segundo por lo tanto el flujo es: F = m/t
1.- F = kg/seg m = masa en kg T = tiempo en seg
2.- m = ρv
2 en 1 F = ρv/t F = ρQ
Principio de Bernoulli
El principio de Bernoulli, también denominado ecuación de Bernoulli o Trinomio de Bernoulli, describe el comportamiento de un fluido moviéndose a lo largo de una línea de corriente. Fue expuesto por Daniel Bernoulli en su obra Hidrodinámica (1738) y expresa que en un fluido ideal (sin viscosidad ni rozamiento) en régimen de circulación por un conducto cerrado, la energía que posee el fluido permanece constante a lo largo de su recorrido. La energía de un fluido en cualquier momento consta de tres componentes:- Cinética: es la energía debida a la velocidad que posea el fluido.
- Potencial gravitacional: es la energía debido a la altitud que un fluido posea.
- Energía de flujo: es la energía que un fluido contiene debido a la presión que posee.
- V = velocidad del fluido en la sección considerada.
- g = aceleración gravitatoria
- z = altura en la dirección de la gravedad desde una cota de referencia.
- P = presión a lo largo de la línea de corriente.
- ρ = densidad del fluido.
- Viscosidad (fricción interna) = 0 Es decir, se considera que la línea de corriente sobre la cual se aplica se encuentra en una zona 'no viscosa' del fluido.
- Caudal constante
- Flujo incompresible, donde ρ es constante.
- La ecuación se aplica a lo largo de una línea de corriente o en un flujo irrotacional
Aunque el nombre de la ecuación se debe a Bernoulli, la forma arriba expuesta fue presentada en primer lugar por Leonhard Euler.
Un ejemplo de aplicación del principio lo encontramos en el flujo de agua en tubería.
Ecuación de Bernoulli y la Primera Ley de la Termodinámica
De la primera ley de la termodinámica se puede concluir una ecuación estéticamente parecida a la ecuación de Bernouilli anteriormente señalada, pero conceptualmente distinta. La diferencia fundamental yace en los límites de funcionamiento y en la formulación de cada fórmula. La ecuación de Bernoulli es un balance de fuerzas sobre una partícula de fluido que se mueve a través de una línea de corriente, mientras que la primera ley de la termodinámica consiste en un balance de energía entre los límites de un volumen de control dado, por lo cual es más general ya que permite expresar los intercambios energéticos a lo largo de una corriente de fluido, como lo son las pérdidas por fricción que restan energía, y las bombas o ventiladores que suman energía al fluido. La forma general de esta, llamémosla, "forma energética de la ecuación de Bernoulli" es:

donde:
- γ es el peso específico (γ = ρg).
- W es una medida de la energía que se le suministra al fluido.
- hf es una medida de la energía empleada en vencer las fuerzas de fricción a través del recorrido del fluido.
- Los subíndices 1 y 2 indican si los valores están dados para el comienzo o el final del volumen de control respectivamente.
- g = 9,81 m/s2 y gc = 1 kg·m/(N·s2)
Suposiciones
La ecuación arriba escrita es un derivado de la primera ley de la termodinámica para flujos de fluido con las siguientes características.
- El fluido de trabajo, es decir, aquél que fluye y que estamos considerando, tiene una densidad constante.
- No existe cambio de energía interna.


gracias es muy buena =)
ResponderEliminarGracias
ResponderEliminarGamsahabnida
ResponderEliminar